Ciencias Naturales: Movimiento acelerado.

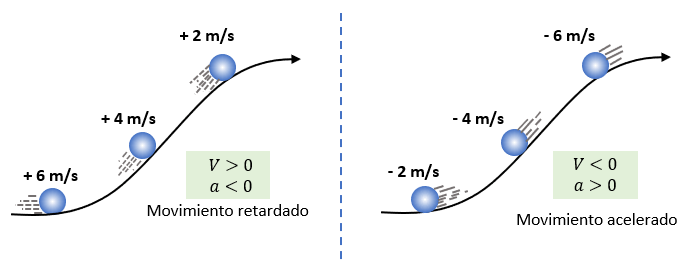
Movimiento acelerado.

En física, todo movimiento uniformemente acelerado (MUA) es aquel movimiento en el que la aceleración que experimenta un cuerpo, permanece constante (en magnitud vectores y dirección) en el transcurso del tiempo manteniéndose firme.

El movimiento rectilíneo uniformemente acelerado, en el que la trayectoria es rectilínea, que se presenta cuando la aceleración y la velocidad inicial tienen la misma dirección.

El movimiento parabólico, en el que la trayectoria descrita es una parábola, se presenta cuando la aceleración y la velocidad inicial no tienen la misma dirección.

En el movimiento circular uniforme, la aceleración tan solo es constante en módulo, pero no lo es en dirección, por ser cada instante perpendicular a la velocidad, estando dirigida hacia el centro de la trayectoria circular (aceleración centrípeta). Por ello, no puede considerárselo un movimiento uniformemente acelerado, a menos que nos refiramos a su aceleración angular.

Movimiento uniformemente acelerado en mecánica clásica

En mecánica clásica el movimiento de una partícula sometida a una fuerza constante resulta ser un movimiento uniformemente acelerado. En el caso más general la trayectoria de una partícula sometida a una fuerza constante resulta ser una parábola.

Para analizar la situación supondremos que se aplica una fuerza constante a una partícula que se mueve inicialmente con velocidad {\displaystyle v_{0}\,}{\displaystyle v_{0}\,}. Sin pérdida de generalidad, podemos suponer que el movimiento se presenta en el plano XY sujeto a las ecuaciones:

B.R.S

{\displaystyle \left\{{\begin{array}{llll}{\ddot {x}}=0&\mathrm {con} \quad x(0)=0&\mathrm {y} \quad {\dot {x}}(0)=v_{0,x}t\\{\ddot {y}}=a_{y}&\mathrm {con} \quad y(0)=0&\mathrm {e} \quad {\dot {y}}(0)=v_{0,y}t\end{array}}\right.}{\displaystyle \left\{{\begin{array}{llll}{\ddot {x}}=0&\mathrm {con} \quad x(0)=0&\mathrm {y} \quad {\dot {x}}(0)=v_{0,x}t\\{\ddot {y}}=a_{y}&\mathrm {con} \quad y(0)=0&\mathrm {e} \quad {\dot {y}}(0)=v_{0,y}t\end{array}}\right.}

Integrando las ecuaciones diferenciales anteriores se tienen las siguientes velocidades y desplazamientos:

{\displaystyle \left\{{\begin{array}{lll}{\dot {x}}(t)=v_{0,x}&\Rightarrow &x(t)=v_{0,x}t\\{\dot {y}}(t)=v_{0,y}+a_{0}t&\Rightarrow &y(t)=v_{0,y}t+{\cfrac {a_{0}t^{2}}{2}}\end{array}}\right.}{\displaystyle \left\{{\begin{array}{lll}{\dot {x}}(t)=v_{0,x}&\Rightarrow &x(t)=v_{0,x}t\\{\dot {y}}(t)=v_{0,y}+a_{0}t&\Rightarrow &y(t)=v_{0,y}t+{\cfrac {a_{0}t^{2}}{2}}\end{array}}\right.}

Para encontrar la ecuación de la trayectoria se despeja el tiempo de la expresión para la coordenadas {\displaystyle \scriptstyle x(t)}{\displaystyle \scriptstyle x(t)} y se substituye {\displaystyle \scriptstyle t(x)}{\displaystyle \scriptstyle t(x)} para obtener {\displaystyle \scriptstyle y(t(x))}{\displaystyle \scriptstyle y(t(x))}:

{\displaystyle y(x)={\frac {v_{0,y}}{v_{0,x}}}x+{\frac {a_{0}}{2v_{0,x}^{2}}}x^{2}}{\displaystyle y(x)={\frac {v_{0,y}}{v_{0,x}}}x+{\frac {a_{0}}{2v_{0,x}^{2}}}x^{2}}

resultado que representa la ecuación de una parábola.

Movimiento bajo fuerza constante en mecánica relativista

En mecánica relativista no existe un equivalente exacto del movimiento uniformemente acelerado, ya que la aceleración depende de la velocidad y mantener una aceleración constante requeriría una fuerza progresivamente creciente. Además desde el punto de vista de la teoría de la relatividad especial no es realista suponer que pueda existir un cuerpo con aceleración constante indefinidamente ya que tras un tiempo suficientemente largo de aceleración uniforme el cuerpo acabaría teniendo una energía cinética infinita (puesto que la masa se haría infinita), lo cual no es realista. Para un cuerpo hipotético partiendo del reposo y sometido a la aceleración constante a, ese tiempo es igual a la c/a (c:velocidad de la luz). Existen dos casos interesantes de movimiento bajo fuerza constante:

Movimiento rectilíneo bajo fuerza constante, este movimiento se caracteriza por una aceleración progresivamente decreciente a medida que el móvil se aproxima más y más a la velocidad de la luz.

Movimiento bidimensional bajo fuerza constante, este es un análogo relativista cercano al movimiento parabólico, sin embargo, la trayectoria nunca es exactamente una parábola, a diferencia de lo que sucede en mecánica clásica.

Movimiento bajo fuerza constante en mecánica cuántica

En mecánica cuántica no se puede hablar de trayectorias ya que la posición de la partícula no puede determinarse con precisión arbitraria, por lo

(*){\displaystyle -{\frac {\hbar ^{2}}{2m}}\left({\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}\right)-xF\psi (x,y,z)=E\psi (x,y,z)}{\displaystyle -{\frac {\hbar ^{2}}{2m}}\left({\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}\right)-xF\psi (x,y,z)=E\psi (x,y,z)}

Donde:

{\displaystyle \hbar \,}\hbar \, es la constante de Planck racionalizada.

{\displaystyle m\,}m\, es la masa de la partícula.

{\displaystyle F\,}F\, es la fuerza que se ejerce sobre la partícula.

{\displaystyle E\,}E\, es la energía de un estado estacionario del hamiltoniano cuántico.

Para ver si es posible encontrar soluciones particulares mediante el método de separación de variables se postula la forma:

{\displaystyle \psi (x,y,z)=\psi _{l}(x)\psi _{t}(y,z)}{\displaystyle \psi (x,y,z)=\psi _{l}(x)\psi _{t}(y,z)}

Donde l es recientemente de longitudinal y t de transversal, ambas funciones pueden relacionarse con la variación en la dirección de la fuerza y en las direcciones transversales a la fuerza. La parte longitudinal {\displaystyle \psi _{l}(x)}{\displaystyle \psi _{l}(x)} viene dada en términos de la función de Aire:

{\displaystyle \psi _{l}(x)=A\mathrm {Ai} \left[\left({\frac {2m}{\hbar ^{2}F}}\right)^{1/3}(Fx+E_{l})\right]}{\displaystyle \psi _{l}(x)=A\mathrm {Ai} \left[\left({\frac {2m}{\hbar ^{2}F}}\right)^{1/3}(Fx+E_{l})\right]}

Nótese que la ecuación anterior tiene solución para cualquier valor de El y por tanto los estados energéticos posibles de una partícula tienen un espectro continuo (a diferencia de lo que pasa para otros sistemas cuánticos con niveles de energía discretos).